樹木が成長するとは

　樹木は光合成を行い、有機物を作り出します。この有機物を使って、枝や幹、根を作ります。光合成で作り出した有機物のすべてが、樹木の成長に利用されるわけではありません。樹木自身が生きていくために呼吸をします。このときに光合成で作り出した有機物を消費します。

　光合成で作り出した有機物の量を総生産といいます。総生産から呼吸による消費分を差し引いたものは純生産と呼ばれます。

　　［純生産量］＝［総生産量］−［呼吸量］　というわけです。

　まだ続きます。樹木が作り出した有機物のうち純生産の部分は、樹木のいろいろな部分を作るのに使われます。すると純生産量が樹木の成長量に等しいと考えてよいでしょうか。残念。葉や枝、根などの一部分は毎年枯れていきます。純生産量のうち一部は、この枯れた量を補うのに使われます。補ってあまった分が成長量ということになります。

　　［成長量］＝［純生産量］−［枯死量］　というわけです。

　高校の参考書から、熱帯雨林と照葉樹林の例をあげてみましょう。
　　　　なお数値の単位は、[kg m^-2 yr^-1]です。

　　　熱帯雨林（高齢林）

　　　　　総生産量（12.32）＝呼吸量（9.24）＋純生産量（3.08）

　　　　　純生産量（3.08）＝枯死量（2.57）＋成長量（0.51）

　　　照葉樹林

　　　　　総生産量（5.17）＝呼吸量（2.87）＋純生産量（2.30）

　　　　　純生産量（2.30）＝枯死量（0.72）＋成長量（1.58）

　この場合、熱帯多雨林の総生産量は照葉樹林の２倍以上という量になっています。

生き物の数はどのように増えるか

ここで、生きものは一般的にどのような成長をするのか考えてみましょう。先ずは生きものの数（個体数）がどのように増えるのか。以下、「ですます」調から「である」調に変更します。

　　　N(t): 時間t におけるある種の個体数　とする。

　　ある短い時間間隔Δt 後には N(t + Δt)に増加するとする。

　　この間の個体数の変化率（内的自然増加率，intrinsic rate of natural increase）　　をr とすると，

      N(t + Δt) = N(t) + r N(t)Δt           (1)

  と表すことができる。
  N(t)を移項した後に，両辺をΔt で割って，

      N(t + Δt) - N(t)
      ----------------- = r N(t)              (2)
             Δt

  と表現できる。
  この式の左辺でΔtを０に近づけると，

      dN(t)/dt = rN(t)                        (3)

  という微分方程式を得ることができる。
  この微分方程式から，

      N(t) = N(0)exp(rt)	              (4)

  という成長曲線が導かれる。

　　指数関数的成長の例

　　(a) ある菌が，条件がよければ15分に1回分裂するとすると，1gの菌は1日後には79×1027gになる。地球の重量が5.97×1027ｇなので，地球の約13倍の重量になる。

　　(b) ねずみの個体数が最初１０匹であった。７日後には１５匹になった。内的自然増加率を求めてみよう。
　(2)式でt=0，Δt=7 とし，N(0)=10，N(7)=15 を代入すると，
　　　　　　 15 - 10
　　　　ｒ＝ --------- ＝ 0.0571／日
　　　　　　　7・12.5
　念のために，(4)式に，N(0)=10，N(7)=15 を代入すると，
　　　15 = 10・exp(7r)
となり，これを解くと　r=0.05792 が得られる。(2)式で得られるrの値は，内的自然増加率の近似値である。

　　さらに7日経つと（14日後）何匹になるだろうか。最初の7日で15/10 = 1.5倍だから，次の7日間にも1.5倍になると期待できる。したがって，15×1.5 = 22.5匹になる。
　さらに念のため，(4)式で N(0)=10，r=0.05792，t=14 とすると，
　　　N(14) = 10・exp(0.05792×14) = 22.50
となり，等しい値が得られる。

　では，20日後の個体数は何匹になるのだろうか？(2)式と(4)式のどちらを使うのが便利なのだろうか？

(a)上の菌の増殖の例について，菌の重さの変化をグラフに描きなさい。ただし，最初の3時間の変化のみを描きなさい。まずは表を作ってみよう。
時間　　（分）　0 15 30 45 60 75・・・・・・・・・240
菌の重さ（ｇ）　1 2 4 8 16 32・・・・・・・・・???
また，このときの内的自然増加率を計算しなさい。

(b) 豊臣秀吉から欲しいものをやると言われて，曾呂利新左衛門は将棋版を指して「今日は一粒、明日二粒、三日目は四粒と、前日の倍にして盤の目の数、81日分の米粒をいただきたい」と答えた。おやすい御用と受けた秀吉。さて実際にやってみると、日本中の米を集めても足りなくなりました。

(c) ある水草が池にあるとする。1個体の水草は1時間に2個体に分裂するとする。昼の1時に見たときにちょうど池全体を埋め尽くしたとすると，池の半分を占めていたのは何時間前か？

(d) ある細菌は8時間にその個体数を倍加することが観測される。その成長率（内的自然増加率）はいくらか？近似値でない値を求めよ。単位は[hr^-1]とし，少数以下4桁まで求めなさい。

(e) ある国のG.N.P.（国民総生産）は，2000年1月1日から2001年1月1日の間に6.4%増加した。もしその比率が続くならば，G.N.P.が2倍になるのは何年か？

成長曲線について

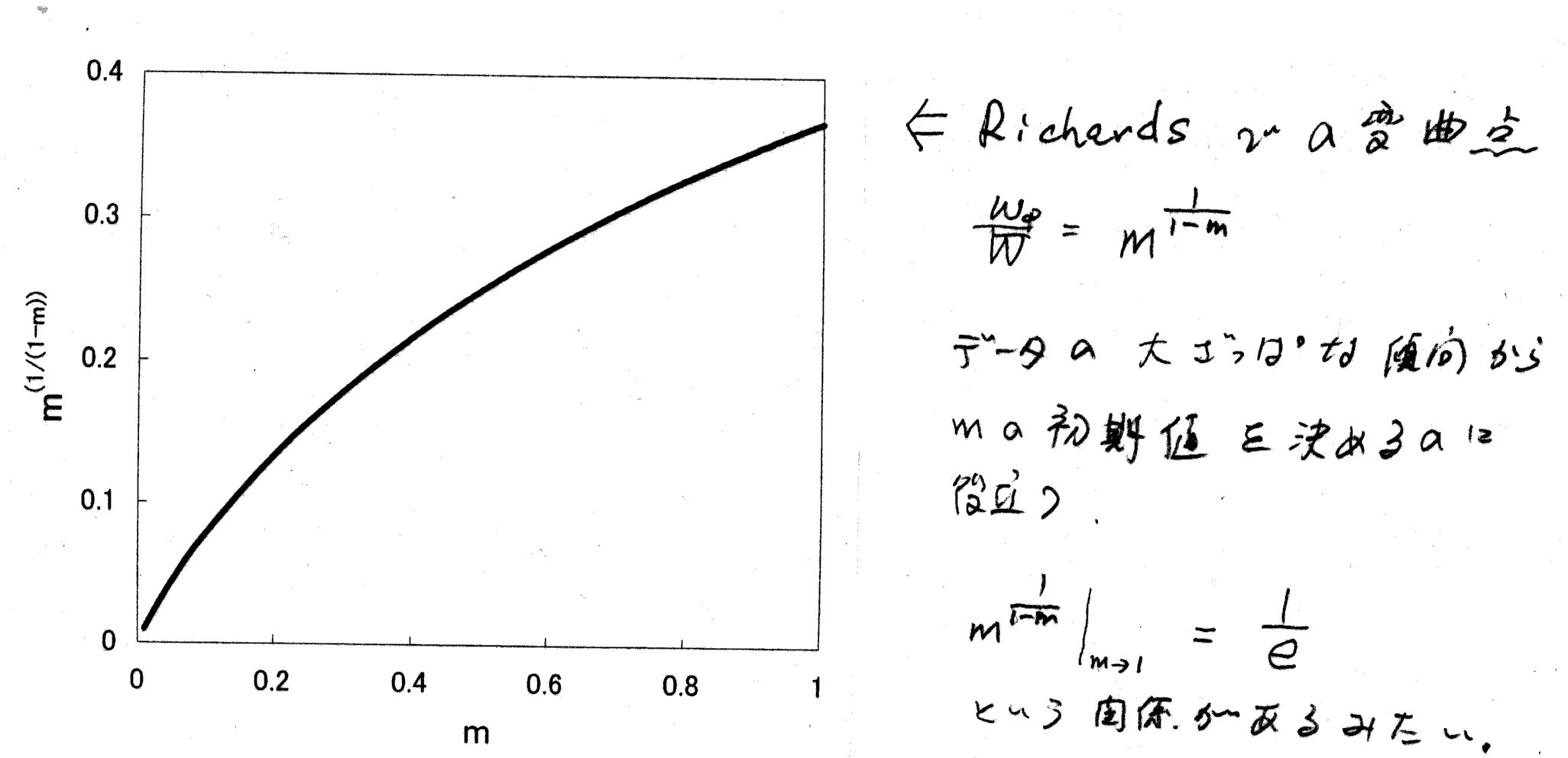
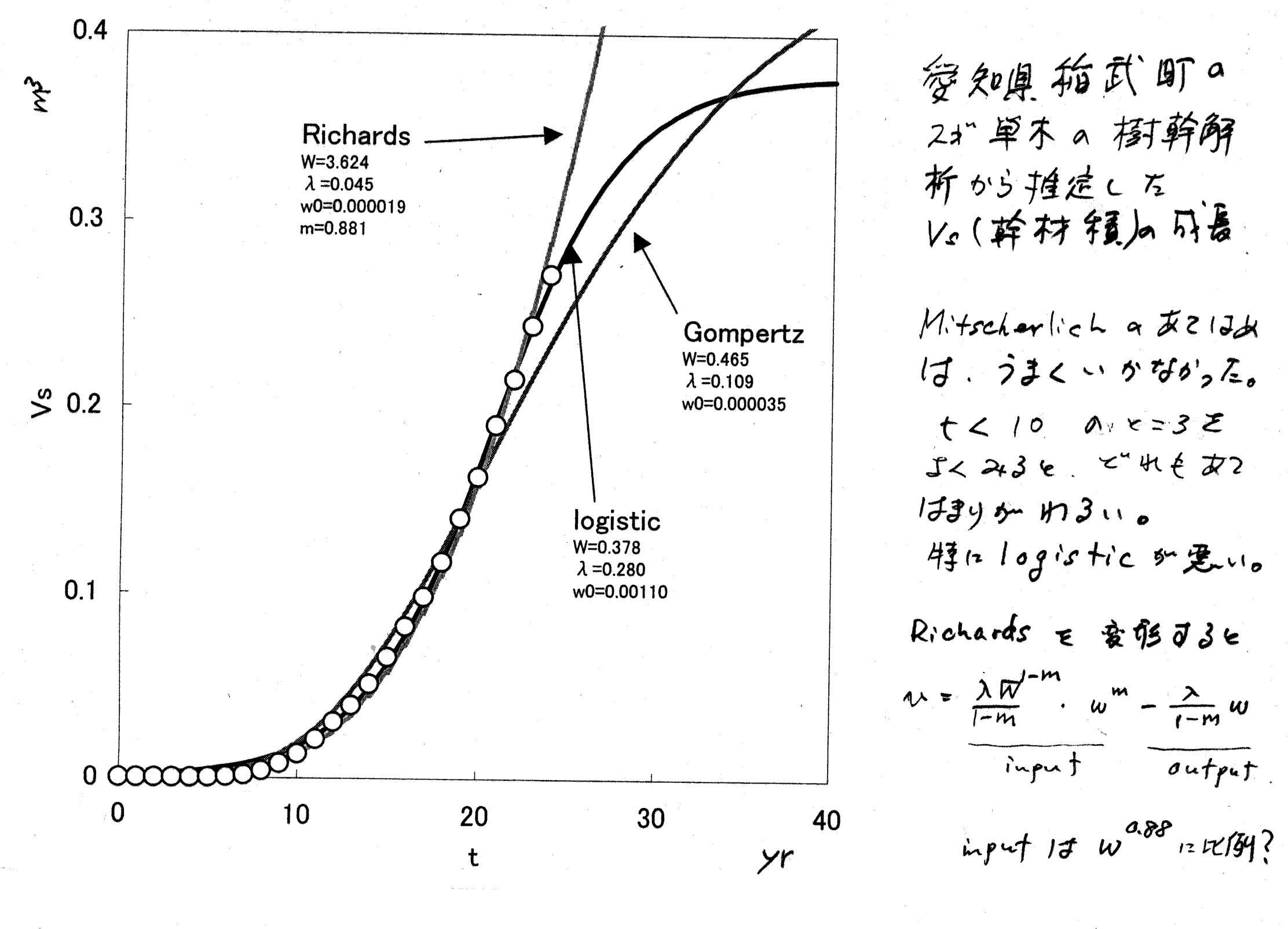
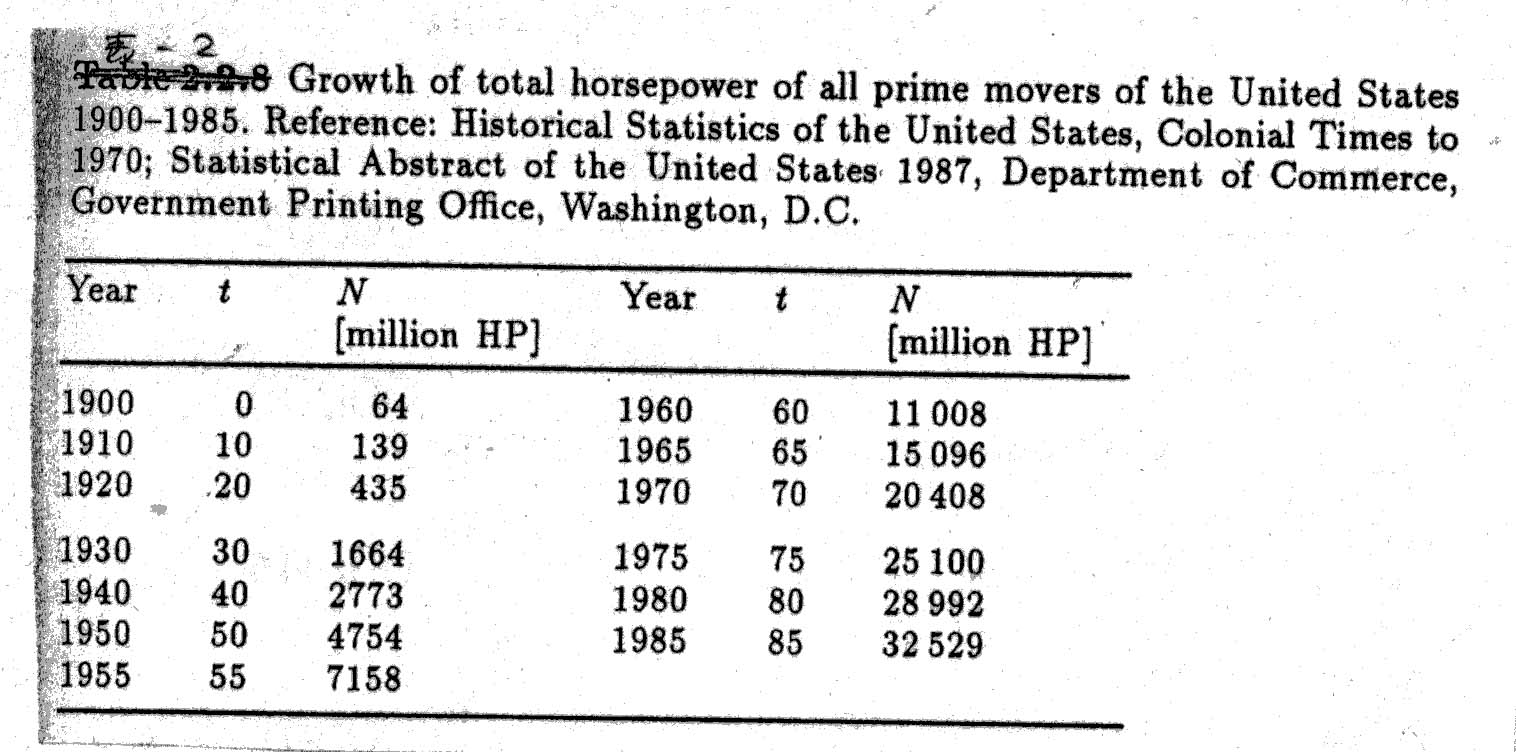←このデータにLogisticとGompertzをあてはめてみる。

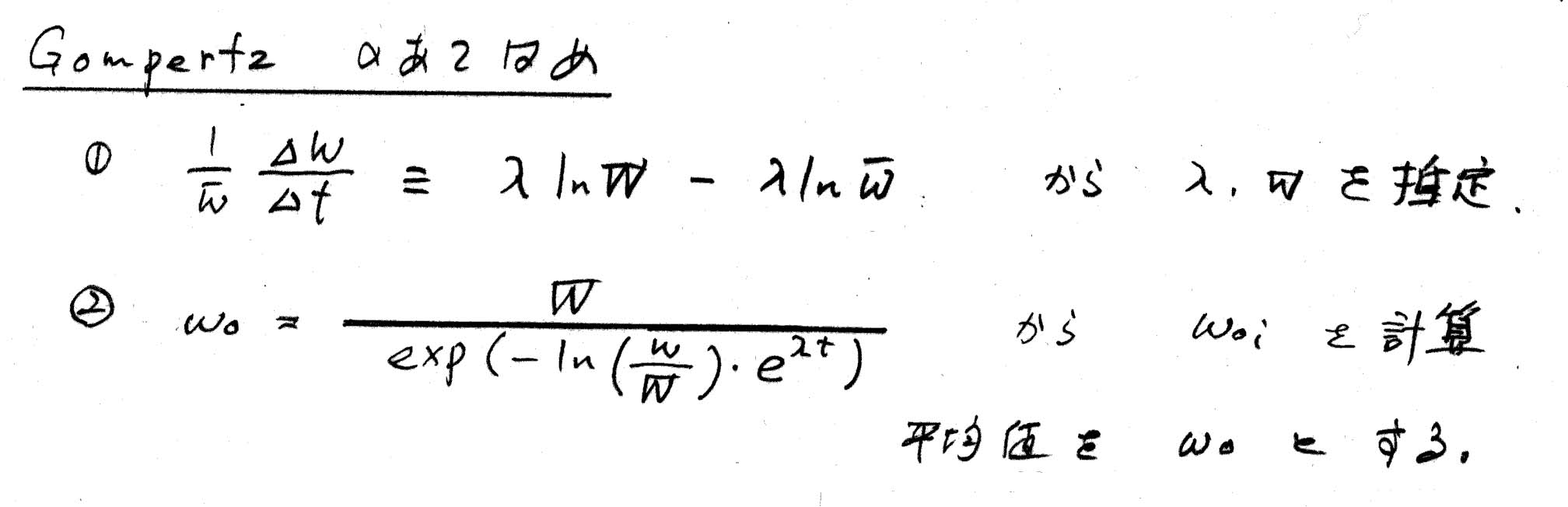
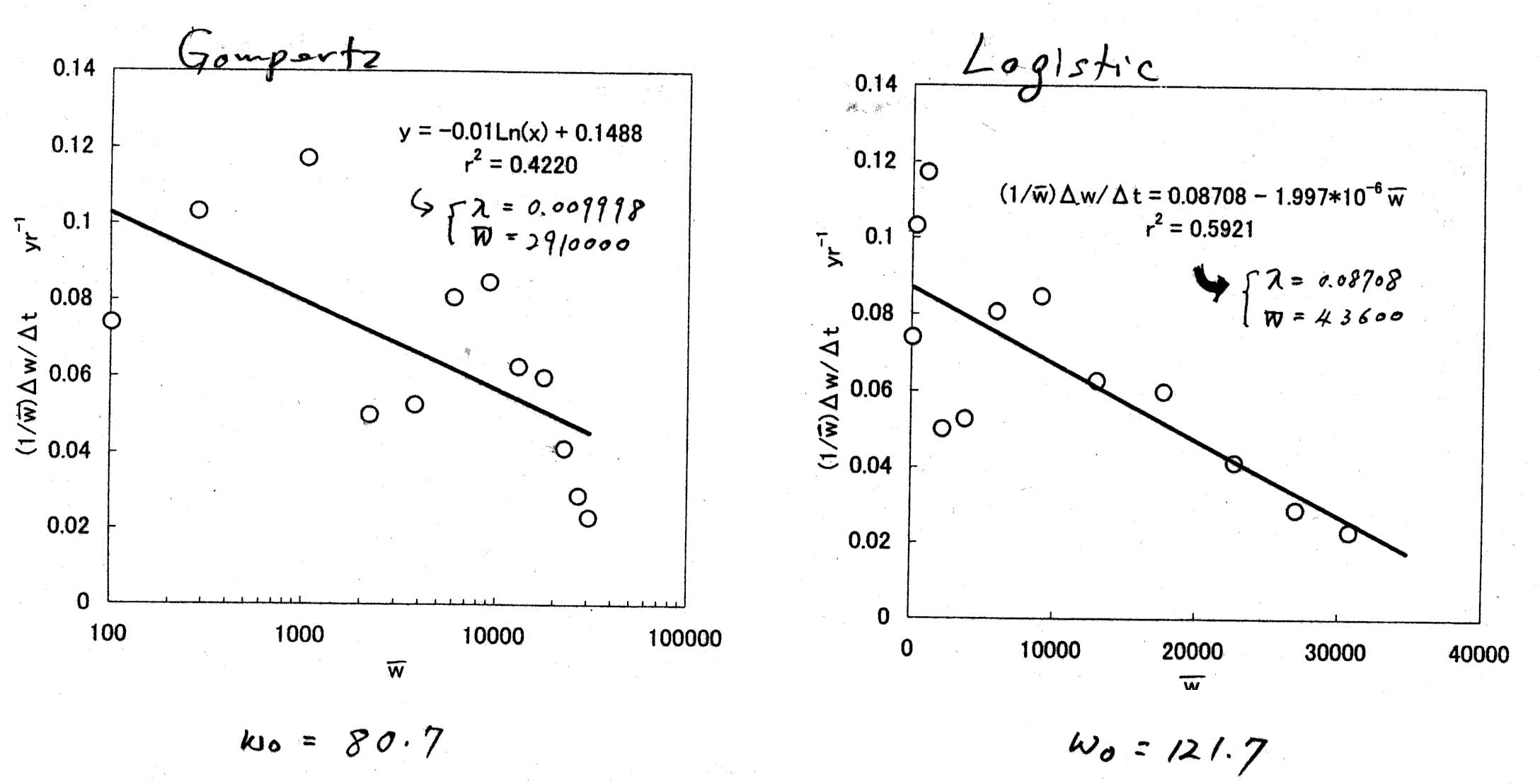
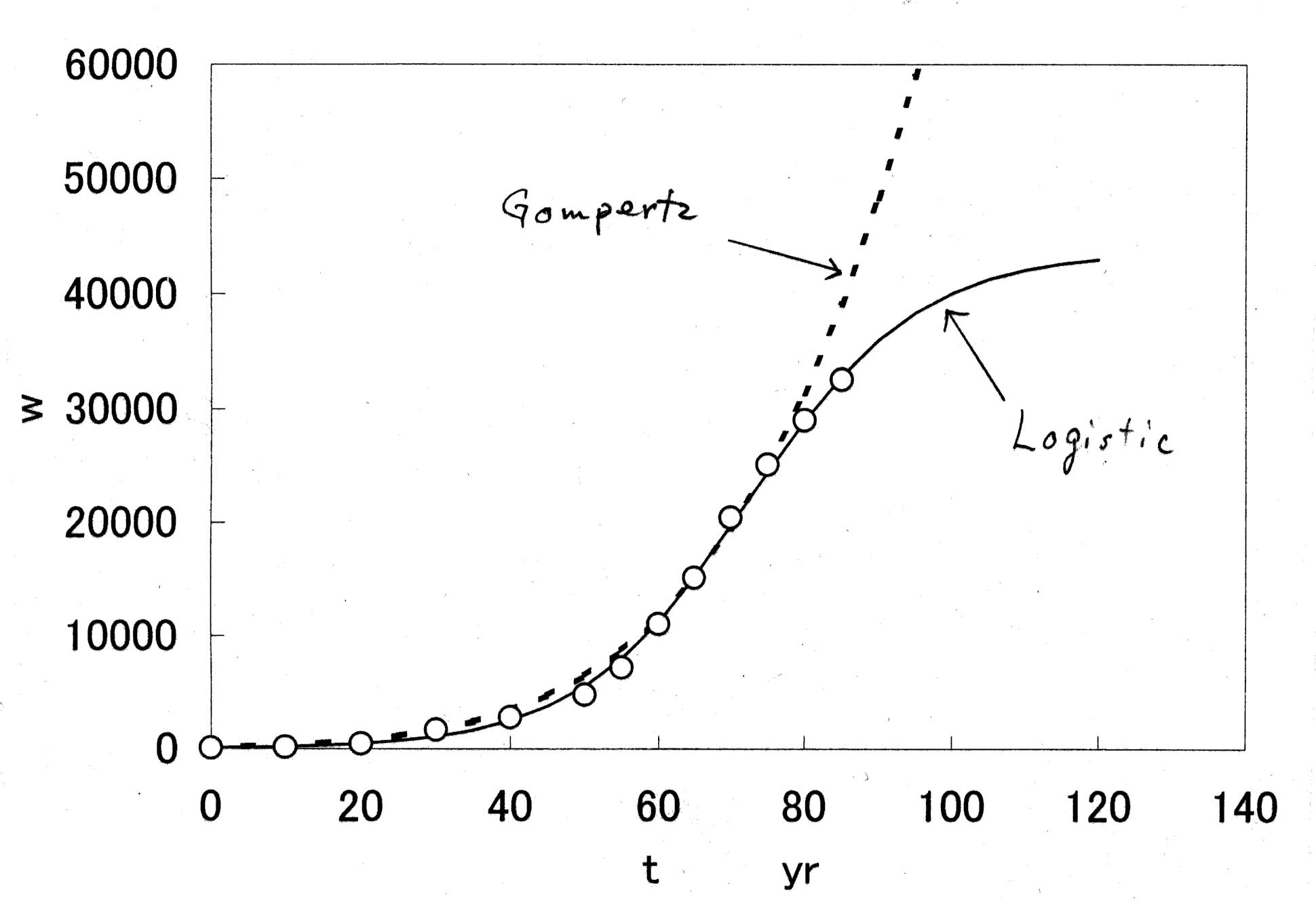
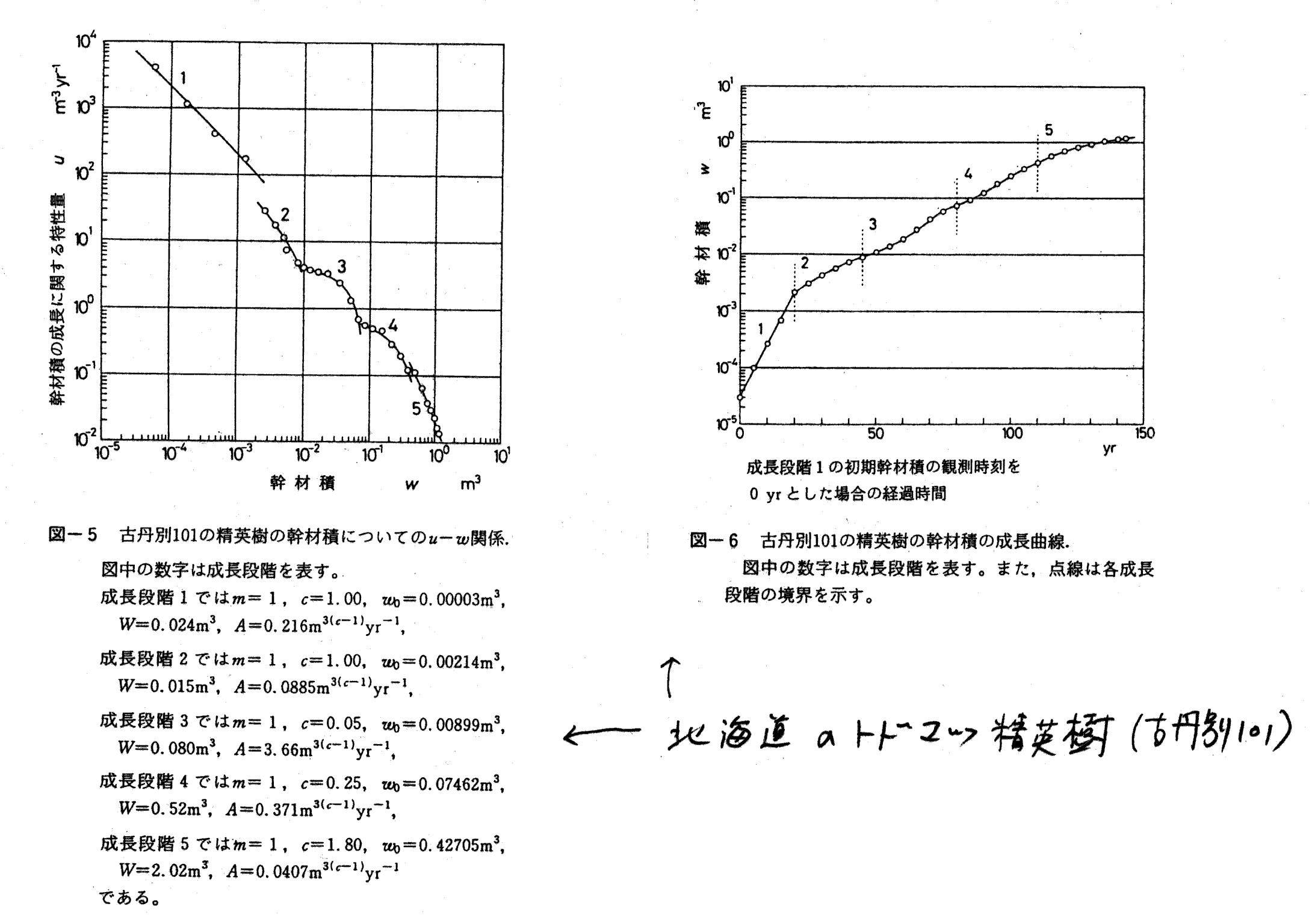
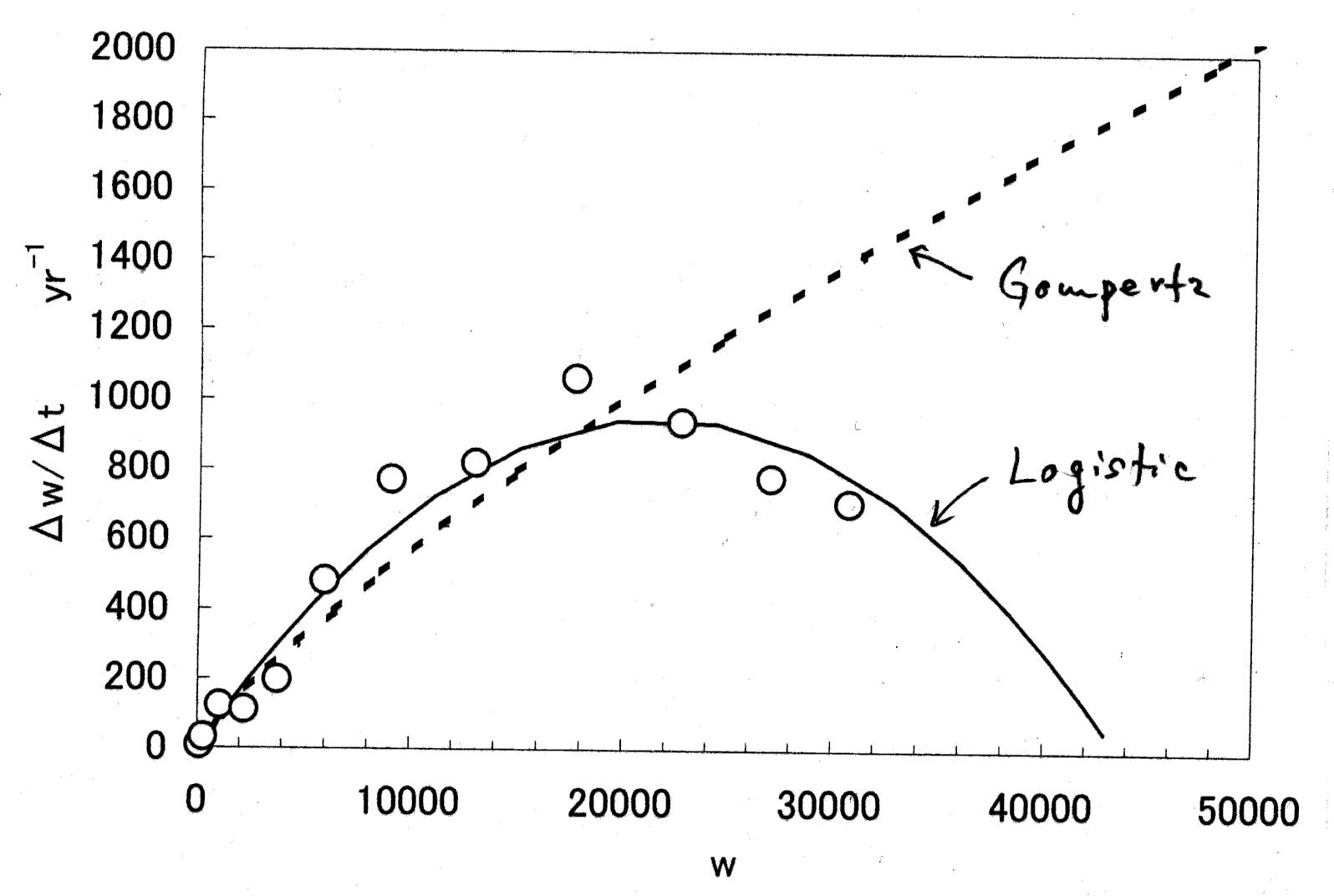← v-w diagram